Mathematikelite grübelte in Tirol über ungelöste Probleme

Das Hauptziel der CMI Summer School ist es, jungen MathematikerInnen Wissen und Werkzeuge zu vermitteln, sodass sie zukünftig in einem aktiven und wichtigen Gebiet der Mathematik forschen können. Nach Hawaii und Brasilien waren heuer die Tiroler Berge Schauplatz dieser Zusammenkunft. Nicht nur in Größe und Dauer hob sich die Summer School in Obergurgl von ähnlichen mathematischen Konferenzen ab, auch der Ort an dem sie stattfand, ist ungewöhnlich. Obergurgl befindet sich auf 2.000 Metern Seehöhe inmitten der Ötztaler Alpen. Fern von jeglichen Ablenkungen konnten sich die TeilnehmerInnen hier im Universitätszentrum der Universität Innsbruck ausschließlich auf ein Thema konzentrieren.

Ungelöste mathematische Spezialfälle

Die Auflösung von Singularitäten ist ein klassisches Problem aus dem Gebiet der Algebraischen Geometrie. Es lässt sich in zwei Fälle unterteilen: Charakteristik Null und positive Charakteristik. Der erste Fall wurde 1964 von Heisuke Hironaka gelöst, der dafür die Fields-Medaille – oftmals als der "Nobelpreis der Mathematik" tituliert – gewann. Der Fall der positiven Charakteristik ist hingegen bis auf wenige Spezialfälle noch immer ungelöst, und stellt damit eine der großen Herausforderungen in der Mathematik dar.

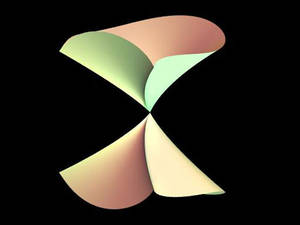	Mit Bildern wie diesen werden algebraische Flächen mit Singularitäten illustriert. Hier ist zum Beispiel die algebraische Fläche "Daisy" dargestellt. (Foto: H. Hauser)

Die Auflösung hat zum Ziel, Singularitäten schrittweise zu eliminieren. Durch gewisse Modifikationen, genannt Blowups, soll die Fläche entfaltet und auseinandergezogen werden – etwa wie das Entwirren eines Wollknäuels –, damit die Singularitäten einfacher und verständlicher werden, bis sie schlussendlich ganz verschwunden sind. Dadurch erhält man eine glatte Fläche, die auf die singuläre Fläche projiziert und diese somit parametrisiert. Solche Parametrisierungen sind von eminenter Bedeutung in zahlreichen Anwendungen innerhalb und außerhalb der Mathematik.

Tägliche Vorlesungen

Die ersten drei Wochen des Programmes boten tägliche Vorlesungen der Professoren Herwig Hauser (Universität Wien und Innsbruck), Josef Schicho (Radon Institut, Linz) und Orlando Villamayor (Universidad Autónoma de Madrid). Von Diskussions- und Übungsstunden begleitet, brachte jeder der Vortragenden dem Publikum verschiedene Aspekte der Auflösung von Singularitäten bis hin zum Problem der Auflösung in positiver Charakteristik näher. Die vierte Woche bot mehrere fortgeschrittene Mini-Vorlesungen zu verschiedenen aktuellen Forschungsthemen – etwas Auflösung von Vektorfeldern und torischen Varietäten (Nash-Blowups).

	Das Vorlesungs-Highlight war zweifellos ein Kurs des mittlerweile 81-jährigen Fields-Medaillenträgers Heisuke Hironaka, der immer noch aktiv auf dem Gebiet forscht und dem jungen Publikum seine Ideen zur Auflösung in Charakteristik p darlegte. (Foto: E. Faber)

Die Summer School wurde vom amerikanischen Clay Mathematics Institute finanziert, mit zusätzlicher großzügiger Unterstützung durch die Universitäten Wien und Innsbruck. (red)