Faszination Bewegungsabläufe

Ob bei der Haddsch – der islamischen Wallfahrt, anlässlich derer jährlich Millionen muslimischer PilgerInnen nach Mekka reisen – oder Musikveranstaltungen wie der Loveparade in Deutschland: Große Menschenmassen entwickeln häufig eine schwer einschätzbare Eigendynamik. Trotz etlicher Sicherheitsvorkehrungen kommt es bei solchen Ereignissen immer wieder zu Massenpaniken und tragischen Unfällen. Seit Juli 2010 beschäftigt sich die Hertha-Firnberg-Stelleninhaberin Marie-Therese Wolfram im Rahmen ihres dreijährigen FWF-Projekts u.a. mit verschiedenen "Crowd Motion"-Ansätzen – wissenschaftlichen Modellen, welche die Bewegungsabläufe großer Menschenmassen zu beschreiben versuchen.

Von Algorithmen und Simulationen

"Ausgehend von Ansätzen der statistischen Physik arbeite ich an der Entwicklung von numerischen Algorithmen. Diese Methoden können auf verschiedene Fragestellungen in anderen Wissenschaftsdisziplinen angewendet werden", erklärt die Mathematikerin Wolfram, die sich im Vorfeld ihres Hertha-Firnberg-Projekts fast zwei Jahre lang an der Universität Cambridge mit sogenannten "Mean Field Game"-Ansätzen beschäftigt hat: "Dabei versuchen wir, effiziente Computersimulationen zu entwickeln, um bestimmte Hypothesen zu überprüfen."

Vom Partikelmodell zum Dichtemodell

Die Grundidee hierbei ist, dass Menschen innerhalb eines großen Menschenflusses ungefähr dieselben Eigenschaften besitzen: "Dies ist natürlich eine starke Vereinfachung der Realität", ist sich die Nachwuchswissenschafterin bewusst. In ihrem Modell wird ein durchschnittlicher Fußgänger als ein Punkt definiert, der sich zufällig bewegt, aber trotzdem einem Ziel folgt. Zusätzlich hat das Teilchen eine gewisse Abneigung gegen enge Räume, es vermeidet also Ballungen.

"Wenn man nun die Anzahl der Punkte gegen unendlich gehen lässt, ist das Ergebnis eine Gleichung, die den Bewegungsablauf der Menschenmenge beschreibt – ein sogenanntes Dichtemodell", veranschaulicht die Mathematikerin: "Einfacher ausgedrückt: Wenn ich eine Menschenmenge von oben betrachte, sehe ich anfangs die einzelnen Personen. Wenn ich mich aber weiter von der Menge entferne, kann ich nur mehr die Verteilung der Personen beobachten. Dichtemodelle sind mathematisch viel leichter zu simulieren als Partikelmodelle, bei denen jedes einzelne Element gemäß seiner Eigenschaften berücksichtigt wird."

Reduktion auf das Wesentliche

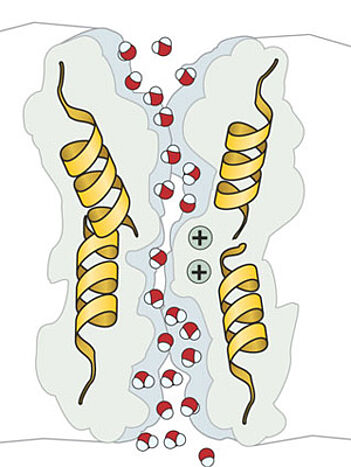
Im Rahmen ihres Projekts wendet Wolfram dieses Prinzip auch auf einen völlig anderen Forschungsbereich an: Mittels Dichteansatz simuliert sie hochkomplizierte biophysikalische Bewegungsabläufe innerhalb von Ionenkanälen. "Es handelt sich dabei um Kanäle in der Zellmembran, die nur gewisse Ionen durchlassen", beschreibt sie das Phänomen. "Zwar gibt es bereits Modelle, die diesen Vorgang sehr detailliert beschreiben – die bereits genannten Partikelmodelle –, jedoch gestaltet sich deren Berechnung als sehr teuer und aufwendig."

Aus diesem Grund versucht die Forscherin, den Ablauf auf die wesentlichen Vorgänge zu reduzieren, um einfachere Simulationen zu ermöglichen. "Auch hier spielen wieder Abstoßmechanismen, ähnlich der Ballungsaversion von FußgängerInnen, eine Rolle. Mathematisch gesehen ist der Übergang vom Partikelmodell zum Dichtemodell – also vom exakten Modell zu einer Wahrscheinlichkeitsverteilung – entscheidend."

Internationale Vernetzung und konkreter Praxisbezug

Die Bedeutung des Ionenkanalmodells liegt auf der Hand: Ist der Ionenaustausch in der Zellmembran eines Menschen gestört, kann es zu Herzrhythmusstörungen kommen. Hingegen liegt eine verlässliche Anwendung des "Crowd Motion"-Ansatzes noch in der Ferne. "Effizientere Modelle führen zu einem besseren Verständnis des Problems", betont die international vernetzte Wissenschafterin, die mit ForscherInnen der Gesellschaft für Schwerionenforschung Darmstadt, der Universität Münster sowie KollegInnen der Universitäten Princeton und Irvine (USA) zusammenarbeitet: "Nur so kann Forschung effektiv gelingen." (il)

Das FWF-Projekt "Mean-field games: Numerik und Anwendung" der Hertha-Firnberg-Stipendiatin Dipl.-Ing. Dr. Marie-Therese Wolfram vom Institut für Mathematik läuft vom 1. Juli 2010 bis zum 1. Juli 2013.